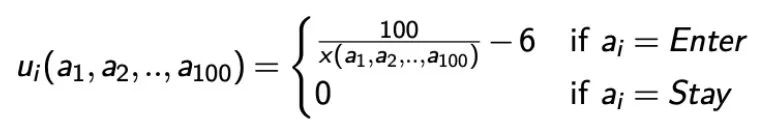Market Entry and the Zero Profit Equilibrium
References quoted & linked below
Game theory analyses situations for individuals/entities using games. A game is a situation in which decisions are interdependent, creating a shared, mutual impact and is displayed on a “matrix". The combination of each “player’s” decision results in a payout, otherwise known as utility (or profit). Typically the higher the number the higher the utility/profit.
4 Minute Read
This is a simultaneous entry game. Payoffs depend on the number of entrants: don’t invest, or enter the market and invest? It illustrates a core prediction of perfectly competitive markets, that profit is driven towards zero, which changes business decisions when weighing the costs and benefits of pursuing a new market. It also shows how expectations about competitor’s behaviour and external forces influences a firm’s decision making process.
The game begins with a new market created by an invention, and any of the 100 firms can simultaneously decide whether to enter the market (or not) by investing $6 million. However, revenue decreases as the number of entrants increases because more firms means more competition on price.
All firms are profit maximising rational actors that have full information about the game, the rules and the consequences. Firms cannot communicate or interact with one another. Outcomes can’t be deviated from, but hypothetically we can test whether unilateral deviations would be profitable.
Should a firm venture its capital? And what is the point where firms are profit maximising and no firm will deviate from said option?
1. The entry game involves 100 potential firms
2. A firm can decide to either enter (invest) or stay (not invest).
Market Entry
3. Entering the market requires that a firm invest $6 million
4. Revenue decreases as the number of entrants rises
5. X = number of entrants
6. The revenue for each entrant is 100 / x.
7. The profit is revenue - cost: 100 / x - 6
- If 17 firms enter, 100 / 17 - 6 < 0, so if more than 16 firms enter, there would be negative profit, so firms who enter would deviate and exit the market.
- If 15 firms enter, 100 / 15 - 6, > 0, so if less than 16 firms enter, there would be profit, and firms who didn’t invest would deviate too and invest.
- If exactly 16 firms enter, 100 / 16 - 6, firms earn 0.25. This is the Nash equilibrium. Leaving gives 0. So insiders stay. Any firms who want to enter the market will increase the number of firms to ≥ 17 and cause everyone - including themself, with negative profit on their balance sheet. Thus, at exactly 16 firms entering the market with 84 not entering, no firm will deviate.
16 firms is a stable, pure strategy Nash equilibrium whereby no player can gain an advantage by changing a strategy.
Credit to my lecturer, Toru Suzuki for the matrix!